The Swinging World

*Welcome to the Swinging World & the Behavior Community*

Swinging Types provide a specification and verification formalism for designing software in terms of many-sorted logic. Current formalisms, be they set- or order-theoretic, algebraic or coalgebraic, rule- or net-based, handle either static system components (in terms of functions or relations) or dynamic ones (in terms of transition systems) and either structural or behavioral aspects, while swinging types combine equational, Horn and modal logic for the purpose of applying computation and proof rules from all three logics.

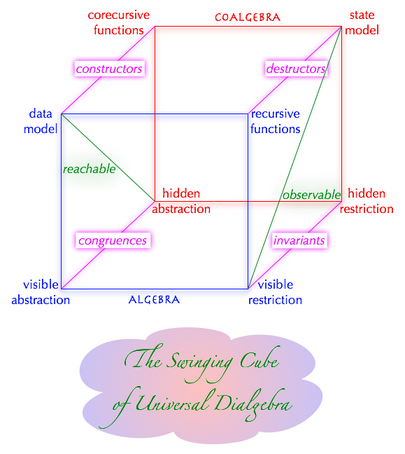
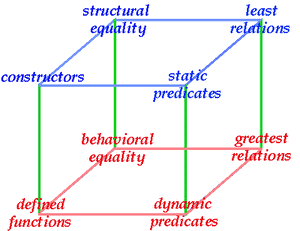
A swinging specification separates from each other visible sorts that denote domains of data identified by their structure; hidden sorts that denote domains of data identified by their behavior in response to observers; predicates (least relations) representing inductive(ly provable) properties of a system; and copredicates (greatest relations) representing complementary ``coinductive'' properties, which often describe behavioral aspects ``in the infinity''.

A model that combines static with dynamic features and structural with behavioral aspects of a system is obtained naturally if all involved entities (objects, states, etc.) are presented as terms built up of constructors for visible or hidden sorts and if functions are specified by conditional equations (= functional programs), least relations by Horn clauses (= logic programs or transition system specifications) and greatest relations by co-Horn clauses. Term equivalences are either structural or behavioral, the former being least, the latter being greatest solutions of particular axioms derived from the type's signature.

Standard models of a swinging type

This integrating approach evolved from 25 years of research and development in the area of formal methods for software construction. It aims at keeping the balance between a wide range of applications and a simple mathematical foundation. To this end boundaries between many research communities had to be crossed. Swinging types employ concepts, results and methods from many-sorted and modal logic, algebraic specification, term rewriting, automated theorem proving, structural operational semantics, functional and logic programming, fixpoint and category theory, universal algebra and coalgebra. Whatever was adopted from these areas, could be reformulated in terms of many-sorted logic with equality.

Papers

[1] Peter Padawitz, Swinging Types = Functions + Relations + Transition Systems, Theoretical Computer Science 243 (2000) 93-165

report version: 61 pages; last update: December 2, 1999; A4 format letter format

This paper mainly presents the theoretical foundations of swinging types, such as standard (term) models, criteria for structural and behavioral consistency, and proof rules. Swinging types admit flexible design guidelines, tailored to particular objectives or application fields. Suitable design methods may be based upon this and the companion paper (5) that explores various application areas and illustrates how swinging types realize different programming or specification styles. As to structuring concepts for swinging types, parameterization and genericity are involved in this paper, while (2) and (3) deal with hierarchical algebraic/coalgebraic specifications, conservative extensions and refinements.

Contents: 1 Introduction - 2 The syntax of swinging types - 3 Structures and congruences - 4 Functionality, fixpoints, standard models - 5 The final model and hierarchy conditions - 6 Coinductive axioms - 7 A modal invariance theorem - 8 Conclusion

[2] Peter Padawitz, Dialgebraic Specification and Modeling slides

last update: May 7, 2007 (DRAFT)

Dialgebraic specifications combine algebraic with coalgebraic ones. We present a uniform syntax, semantics and proof system for chains of signatures and axioms such that presentations of visible data types may alternate with those of hidden state types. Each element in the chain matches a design pattern that reflects some least or greatest model
construction. We sort out twelve such design patterns. Six of them lead to least models, the other six produce greatest models. Each construction of the first group has its dual in the second group.

[3] Peter Padawitz, Structured Swinging Types

45 pages; last update: August 30, 2005 (DRAFT)

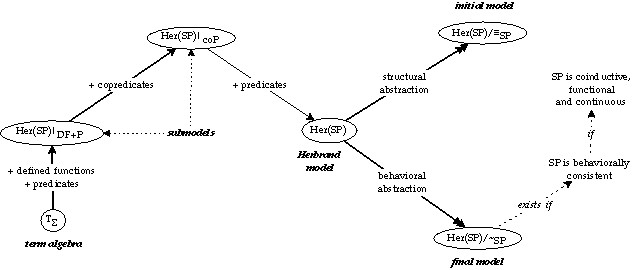
Swinging types (STs) are an axiomatic specification formalism for designing and verifying software in terms of many-sorted logic and Herbrand models. STs are one-tiered insofar as static and dynamic, structural and behavioral aspects of a system are treated on the same syntactic and semantic level. Since the Herbrand models are collections of least and greatest relational fixpoints, all testing or verifying of the specification can be reduced to deductive processes, from unfolding functions or relations via simplifying functional normal forms or logical sentences to inductive or coinductive proofs.

Swinging types were introduced in [1]. The paper at hand equips STs with a notion of hierarchy that admits stepwise modular developments. Semantically, the hierarchy leads to {\it stratified Herbrand models}. Hierarchical specifications also suggest a syntactical difference between axioms of the basic part and axioms of the actual extension: basic specifications admit only Horn clauses, while extensions may involve generalized Horn clauses with implications and universal quantifiers in the premise as well as co-Horn clauses that specify greatest fixpoints. In a further development step, an extension is translated into a logically equivalent Horn specification that becomes the basic part of a higher level.

Secondly, distinguished constructors, called object constructors extend the possibilities for axiomatizing behavioral equalities, which allows us to build constructor-based types on top of observer-based ones. Standard object constructors are the tupling operators for product sorts and injections for sum sorts.

Thirdly, STs are equipped with a simple and intuitive notion of refinement for ``implementing'' a swinging type in terms of another. Due to the one-tieredness of STs refinements allow us to decompose atomic states into composite ones, to simulate a visible sort with structural equality by a hidden sort with behavioral equality, or to replace a global I/O relation by local message-passing state transitions. We present and apply a powerful and completely deductive criterion for refinement correctness.

[4] Peter Padawitz, Basic Inference Rules for Algebraic and Coalgebraic Specifications A4 format letter format

22 pages; last update: May 28, 2001

We give a survey of proof and computation rules that evolved from our many years' experience with formal design methods and that proved to be necessary and sufficient for executing as well as verifying algebraic or coalgebraic data type specifications. Based on many-sorted logics, swinging types provide a uniform syntax and the semantics with respect to which the rules are sound and, to a certain extent, complete.

See also

[5] Peter Padawitz, Swinging Types At Work

99 pages; last update: April 11, 2003 (under revision!)

We present a number of swinging specifications with visible and/or hidden components, such as lists, sets, bags, maps, monads, streams, trees, graphs, processes, nets, classes, languages, parsers,... They provide more or less worked-out case studies and shall allow the reader to figure out the integrative power of the swinging type approach with respect to various specification and proof formalisms. For instance, the translation of algebraic Petri nets into swinging types admits the generalization of net proof methods and thus---via a compiling graph grammar---for verifying SDL specifications. Similarly, UML class diagrams and state machines are turned into swinging types in order to make them amenable to constraint solving and proving.

[6] Peter Padawitz, Swinging UML: How to Make Class Diagrams and State Machines Amenable to Constraint Solving and Proving, Proc. UML 2000, Springer LNCS 1939 (2000) 162-177

24 slides; last update: September 30, 2000

UML provides a collection of object-oriented pictorial specification techniques, equipped with an informal semantics, but hardly cares about consistency, i.e. the guarantee that a specification has models and thus can be implemented. To achieve this goal and to make verification possible a formal semantics is indispensable. Swinging types (STs) have term models derived from the specifications. The paper takes first steps towards a translation of class diagrams, OCL constraints and state machines into STs. Partly, we proceed along examples, partly we describe generally how, e.g., classes can be turned into signatures.

Swinging types are particularly suitable for interpreting UML models because they integrate static and dynamic components. UML treats them separately, STs handle them within the same formalism. Hence, one may check, for instance, whether static operations are correctly refined to local message passing primitives.

A crucial point of a formal semantics of UML models is a reasonable notion of state. If constraints involve static data as well as states and state transitions, the modal-logic view on states as (implicit) predicates is less adequate than the ST representation as terms denoting tuples of attribute values, ``histories'' of object manipulations or compositions of substates (composite states).

Contents: 1 Introduction - 2 UML and algebraic specification - 3 Refinements - 4 From classes to signatures - 5 On constraints - 6 Adding state machines - 7 Conclusion

Behavior Discussion List	OBJ Language Family	Hidden Algebras
Maude and Maude 2.0	CafeOBJ	Coalgebra Network